Die Erhöhung der Fertigungsgenauigkeiten ist immer ein wichtiges Thema. Interessant wird es dann, wenn dies mit bestehenden Maschinen gelingt und auch die Taktzeit unbeeinflusst bleibt. Mit Methoden des Machine Learnings können in der Serienfertigung noch erhebliche Potenziale genutzt werden: „Nur“ mit Software, Methodik und dem richtigen Know-how.
Konkurrierende Anforderungen an Roboter als Dilemma in der Serienfertigung
Bei der Entwicklung, in der Fertigung und im produktiven Betrieb von Maschinen und Anlagen in der industriellen Fertigung gibt es vielfältige Anforderungen. Zwei zentrale Anforderungen stehen dabei häufig miteinander in einem Konkurrenzverhältnis, zu deren Erfüllung i. d. R. ein Kompromiss eingegangen werden muss:-
- Erfüllung von Qualitätsanforderungen, wie z. B. geringe Fertigungstoleranzen und geringe Toleranzschwankungen von Teil zu Teil
- Effiziente Fertigung zu möglichst wirtschaftlichen Bedingungen, wie z. B. die Herstellung auf günstigeren „Standardmaschinen“ und mit möglichst hoher Ausbringung, also geringer Taktzeit
Kriterien bei der Auswahl von Robotern
Bei der Auswahl eines für eine spezielle Fertigungsaufgabe einzusetzenden Roboters sind vor allem folgende Kenngrößen relevant:
- Geometrische Kenngrößen (mechanische Systemgrenzen, Abmessungen, Arbeitsraum, Freiheitsgrade, …)
- Belastungskenngrößen (Nennlast, max. Nutzlast, Nennmoment, …)
- Kinematische Kenngrößen (Beschleunigung, Verfahrgeschwindigkeit, Verzögerung, …)
- Genauigkeitskenngrößen (Wiederholgenauigkeit, Positioniergenauigkeit)
Nach Bestimmung der Handlingaufgabe und der Belastungen sind es vor allem die geforderten Fertigungstoleranzen und Taktzeiten, welche die Anforderungen an die Genauigkeit und die Kinematik des Roboters bestimmen. Die daraus resultierenden Eigenschaften des Roboters stehen i. d. R. in Konkurrenz zueinander.
Bei dem Leistungskriterium Genauigkeit eines Industrieroboters (IR) unterscheidet man zwischen der Wiederholgenauigkeit und der Positioniergenauigkeit:
Wiederholungsgenauigkeit
Die Wiederholgenauigkeit (RP/ repeatability of pose and path) gibt die Streuung der IST-Positionierung an, die der Endeffektor des Roboters (das letzte Element der kinematischen Kette) aufweist, wenn er aus einer immer gleichen Ausgangslage auf eine angelernte (geteached) bzw. programmierte Position verfährt, der Roboter also wiederholt die immer gleiche Bewegung ausführt. Dieser Wert weist i. d. R. eine vergleichsweise hohe Genauigkeit auf, da nur wenige veränderliche Störgrößen den Bewegungsablauf beeinflussen können.
Positionierungsgenauigkeit
Die Positioniergenauigkeit (auch Absolutgenauigkeit; AP/ accuracy of pose or path) gibt die Abweichung in Weltkoordinaten an, nach Fahrten auf eine – ausgehend vom Roboterkoordinatensystem berechneten – nicht angelernte beliebige Position. Dieser Wert weist i. d. R. im Vergleich zur Wiederholgenauigkeit eine deutlich geringere Genauigkeit auf. Die Absolutgenauigkeit wird durch viele Faktoren des kinematischen Modells des Roboters beeinflusst (z. B. Längen- und Winkelfehler zwischen den Robotergliedern, variable Lasten des Werkstücks). Außerdem weist die Positioniergenauigkeit, betrachtet über den gesamten Arbeitsraum des Roboters, nicht den gleichen Wert auf, sondern kann deutlich variieren. Bei der Entwicklung von Applikationen für Roboter sollten deshalb möglichst angelernte Positionen angefahren werden. Es gibt jedoch Fälle, bei denen nicht jede Position angelernt werden kann, z. B. wenn der Roboter aufgrund der Art des Prozessschrittes immer wieder eine andere Position anfahren muss. Hierfür werden üblicherweise nur drei Positionen angelernt anhand derer das Roboterkoordinatensystem aufgespannt wird. Nun kann die Steuerung beliebige Punkte innerhalb dieses Koordinatensystems dynamisch berechnen und anfahren.
Fallbeispiel: Optimierung der Positioniergenauigkeit bei einem SCARA-Roboter
Roboterapplikationen, bei denen beliebige Positionen im Arbeitsraum mit einer hohen Genauigkeit angefahren werden sollen, bereiten oft Probleme, denn das Erreichen einer hohen Positioniergenauigkeit bei gleichzeitig dynamischem Fahrverhalten gelingt nur selten optimal. Roboterhersteller sind auch deshalb bei der Angabe zu konkreten Positioniergenauigkeiten eher zurückhaltend. Wird jedoch vom Kunden eine spezifische Positioniergenauigkeit gefordert, korreliert das häufig mit einem deutlichen Anstieg in der Preisklasse des Roboters. In manchen Fällen könnte durch die Reduzierung der Geschwindigkeit eine Verbesserung bezüglich der Positioniergenauigkeit erzielt werden. Das entspräche dann allerdings nicht mehr den Vorgaben bezüglich der Taktzeit. Wünschenswert wäre deshalb ein softwarebasiertes Verfahren, um die Positioniergenauigkeit zu verbessern, ohne nachteiligen Einfluss auf die Dynamik (Geschwindigkeit) und damit die Taktzeit. Das wäre zum einen interessant für neue Anwendungsfälle, weil hier günstigere Standardroboter eingesetzt werden könnten, welche durch die Software-Optimierung den „höheren“ Anforderungen gerecht werden könnten. Zum anderen könnten so aber auch bestehende Anlagen nachgerüstet werden, um die Genauigkeit (höhere Qualität) zu steigern bzw. die Taktzeit (kürzere Durchlaufzeit, höhere Stückzahl) zu verkürzen. Eine solche Aufgabenstellung hat sich bei einem unserer langjährigen Kunden (Firma Manz AG, Reutlingen) ergeben. So haben wir im Rahmen eines gemeinsamen Projektes die Möglichkeit zur Optimierung der Positioniergenauigkeit bei gleichzeitiger Einhaltung der Taktzeit mithilfe eines softwarebasierten Verfahrens ermittelt und die Tauglichkeit des Einsatzes im industriellen Bertrieb überprüft.
Zielsetzung: Entwicklung einer generischen Software, welche die Positionierungsgenauigkeit von verschiedensten Robotertypen optimieren kann.
Betrachtet wurde ein sog. SCARA-Roboter (Selective Compliance Assembly Robot Arm) des Roboterherstellers Stäubli. Dies ist eine spezielle Bauform eines Roboters, dessen Aufbau einem menschlichen Arm ähnelt und daher auch als horizontaler Gelenkarmroboter bezeichnet wird. Diese Art von Roboter wird in vielen Anwendungsfeldern in der Industrie eingesetzt, z. B. beim Schweißen, Kleben, Fräsen, Bohren, Biegen, Montieren etc. und für vielfältige Handlingaufgaben.

Lösungsansätze
Versuchsaufbau
Bei dem Vorhaben, die Positioniergenauigkeit zu verbessern, ist neben den in den Achsen der Robotergelenken verbauten Lagesensoren ein weiteres Messsystem erforderlich, welches die tatsächliche Positionierung in Weltkoordinaten und somit auch den Fehler ermitteln kann. Es wird sowohl in der Entwicklung, als auch bei der späteren Evaluierung eines Korrektursystems benötigt. Die industrielle Bildverarbeitung ist dafür wie geschaffen. Deshalb haben wir uns für eine am Endeffektor befestigte Industriekamera entschieden, welche mittels Bildverarbeitung die tatsächliche („wahre“) IST-Position bestimmen kann. Für unsere Roboterapplikation war vor allem die genaue Positionierung auf der Z-Ebene von zentraler Bedeutung. Deshalb haben wir das Problem auf zwei Dimensionen reduziert (X- und Y-Achse) und mussten daher auch nur 2D-Messungen durchführen, welche mit gewöhnlichen Kameras ohne Tiefenmessung problemlos funktioniert.


Roboter mit Kamerasystem; Erkennung der Abweichung zwischen IST- zur SOLL-Position
Für das Problem existieren zwei grundsätzlich unterschiedliche Lösungsansätze
1. Beim klassischen Vorgehen aus dem Maschinenbau würde man die durch das kamerabasierte Messsystem gewonnenen Informationen über den Positionierungsfehler verwenden, um einen Regelkreis aufzubauen. Der Regelkreis würde den Roboterarm solange nachregeln, bis er die gewünschte Position – mit der Begrenzung auf die Genauigkeit der Kamera – erreicht hat.
2. Wir haben uns jedoch für einen Lösungsansatz mit der Methode des datengetriebenen Machine Learnings entschieden, da dieser einige entscheidende Vorteile gegenüber der klassischen Lösung des Nachregulierens aufweist. Wir folgen damit dem Paradigmenwandel des Machine Learnings von „Algorithmus → Daten → Entscheidung“ hin zu „Daten → Algorithmus → Entscheidung“. Das bedeutet für den konkreten Anwendungsfall, dass wir zunächst Daten sammeln mussten, um im Anschluss daran anhand der Daten einen Algorithmus zu entwickeln bzw. zu trainieren, welcher eine Entscheidung treffen kann und damit den Prozess optimiert.


Lösung
Die grundlegende Idee besteht darin, ein Machine Learning Modell nach einer korrigierten Position in X- und Y-Richtung zu fragen, bevor eine dynamische Position angefahren wird. Der Endeffektor wird dann genauer über der gewünschten Position platziert. Doch wie kommen wir zu so einem Modell? Es gibt verschiedene Machine Learning Methoden (z. B. Lineare Regression, Support Vector Machines, Random Forest, Neuronale Netze), die alle nach demselben „Lern“-Prinzip arbeiten. Indem man diese Methoden mit einem Datensatz trainiert, lernen sie das Verhältnis zwischen Eingangsdaten (sog. „Features“) und Ausgangsdaten (sog. „Label“). Ein Algorithmus optimiert die Modellparameter also so weit, damit das trainierte Modell den Output möglichst genau vorhersagen kann. Je nach Auswahl der Methode können beliebig komplexe Entscheidungsfunktionen approximiert werden. Die Herausforderung liegt in der Auswahl und Konfiguration der am besten für das Problem geeigneten Methode. Denn ein Machine Learning Modell ist nur dann erfolgreich, wenn es das dem Trainingsdatensatz zugrunde liegende Problem „erkennt“ und es generalisieren kann, um auch für neue Daten die richtigen Entscheidungen zu treffen. Einfaches „auswendig lernen“ liefert kein verwertbares Ergebnis. Dann beschreibt es zwar die Trainingsdaten perfekt, der Transfer auf neue Anwendungsfälle wird jedoch scheitern.

Mit diesem Lösungsansatz betrachten wir das Problem der Positionierungsoptimierung als Black-Box. Wir sind nicht darin interessiert, die genauen Ursachen für den Positionierungsfehler ausfindig zu machen. Das Machine Learning Modell übernimmt das für uns im Abstrakten während des Trainings und liefert uns lediglich einen Gesamtkorrekturwert.
Erster Schritt: Daten sammeln
Im ersten Schritt steht die Datenerfassung an, um einen Trainingsdatensatz zu erstellen. Alle Daten, hinter welchen eine Korrelation mit dem Problem vermutet werden kann, müssen aufgezeichnet werden. In unserem Fall möchten wir den zu erwartenden Positionierungsfehler vorhersagen, um eine korrigierte SOLL-Position zu berechnen. Wir vermuten eine Korrelation mit den Zielpunktkoordinaten (SOLL-Position), da die Absolutgenauigkeit im Arbeitsbereich variiert. Zusätzlich wählen wir die Startkoordinaten der Bewegung, sowie die Geschwindigkeit als Features des Trainingsdatensatzes aus. Zu jedem Feature-Vektor wird dann noch das Ergebnis der Positionsmessung via Kamera als Label hinzugefügt. Mit unserem Modul „Collect“ zur Datenerfassung aus dem Ecosystem IIoT Building Blocks ist das Aufzeichnen von Daten verschiedener Roboter, Steuerungen und Sensoren mit wenigen Klicks konfiguriert.
Grundsätzlich ist die Generierung der Trainingsdaten im produktiven Normalbetrieb der Maschine realisierbar. Die kamerabasierte Positionsmessung kann jedoch unter Umständen aufwendiger sein. Da wir uns noch in der Ramp-up-Phase befunden haben, konnten wir die Generierung der Daten als „Trockenübung“ realisieren, indem wir mit dem Roboter über eine Kamerakalibrierplatte mit hoch präzise gedruckten Markern gefahren sind, ohne Einsatz eines Werkzeugs oder Greifers.


Ein Steuerungsprogramm hat den SCARA-Roboter von jeweils verschiedenen, zufällig generierten Startpositionen aus auf dynamisch ausgerechnete Positionen (6 x 7 Marker) mit unterschiedlichen Geschwindigkeiten angefahren. Am Zielpunkt angekommen, hat die Bildverarbeitungssoftware die tatsächliche (wahre) Position ermittelt. Die dabei generierten Daten wurden mit dem Modul „Collect“ erfasst und gespeichert.
Zweiter Schritt: Daten visualisieren und Aufstellen erster Hypothesen
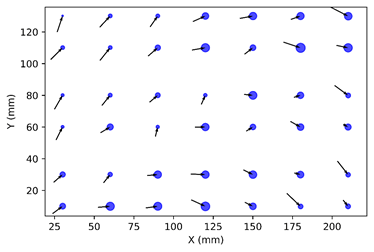
Nachdem der Roboter einige Male über jeden Marker der Kalibrierplatte gefahren ist, haben wir die gespeicherten Daten in eine „Anaconda Python“-Umgebung geladen, dort entsprechend bereinigt und in einen Trainingsdatensatz mit „Feature Vektor“ + „Label“ überführt. Mit der Python Bibliothek „Matplotlib“ haben wir mehrere Plots angefertigt, um die Daten besser zu verstehen und um die Qualität der Features bewerten zu können. Die Abbildung zeigt das Koordinatensystem der Kalibrierplatte. An der Stelle der Marker, die der Roboter angefahren hat, ist der mittlere Fehler durch einen Vektorpfeil eingezeichnet (je länger der Pfeil desto größer der Positionsfehler). Zusätzlich visualisiert die Größe der blauen Kreise die Höhe der Standardabweichung.
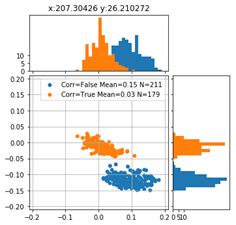
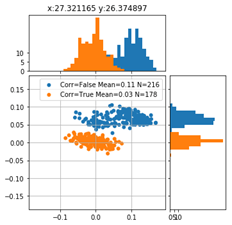
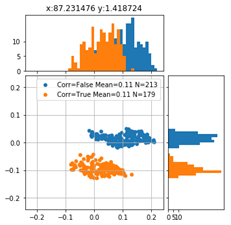
Betrachten wir die Verteilung der Positionierungsfehler des Markers links unten in der Detailauflösung ergeben sich folgende Scatter-Plots:
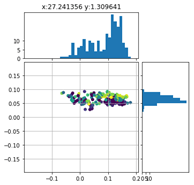
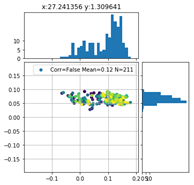
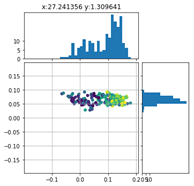
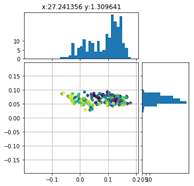
Die Farbe der Punkte repräsentieren jeweils ein unterschiedliches Feature. Vor allem für die X-Koordinate der Startposition ist ein deutlicher Farbverlauf zu erkennen. Die Zeit, also die Verfahrgeschwindigkeit, scheint demgegenüber keinen großen Einfluss auf den Verlauf des Positionierungsfehlers zu haben.
Dritter Schritt: Modellierung
Nachdem die Daten bereinigt, formatiert und zum besseren Verständnis visualisiert wurden, bestand die Herausforderung darin, ein passendes Modell zu finden und mit den Daten zu trainieren. Die Beschaffenheit der Daten beeinflusst maßgeblich die Modellauswahl. Die Modellfreiheitsgrade sollten so dimensioniert sein, dass sie das Problem gerade noch beschreiben können. Beschreiben die Daten zum Beispiel einen linearen Verlauf, tendiert ein Modell, welches Funktionen deutlich höherer Ordnung approximieren könnte, zum Auswendiglernen, aber nicht zum Generalisieren (sog. „Overfitting“). Umgekehrt ist ein Modell mit zu geringen Freiheitsgraden überhaupt nicht in der Lage das Verhalten der Daten zu erfassen (sog. „Underfitting“). Bei größeren Datensätzen (> 3 Dimensionen) gelingt es kaum mehr, auch nicht mit geschickter Visualisierung, die Beschaffenheit der Daten zu begreifen, um dann eine passende Modellfamilie auszuwählen. Die Modellierung erfolgt normalerweise nach dem Trial-and-Error Verfahren. Durch Analyse und Auswertung verschiedener Kenngrößen, wie z. B. der Lernkurve beim Training oder beim Testen des fertig trainierten Modells anhand eines zunächst vorenthaltenden Testdatensatzes, kann die Qualität eines Modells bestimmt werden. Wir haben zunächst verschiedene Modelle ausprobiert und miteinander verglichen, unter anderem ein Lineares Regressions-Modell mit verschiedenen Konfigurationen und unterschiedliche neuronale Netz-Architekturen. Die besten Ergebnisse erzielte dabei ein neuronales Netz mit „2-hidden layer 16-10“. Wir verwendeten dieses Netz, um jeweils ein Modell für X- und Y-Korrekturwerte zu trainieren.
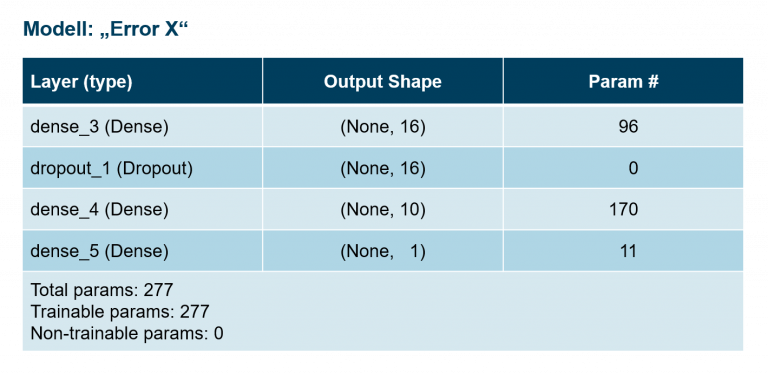
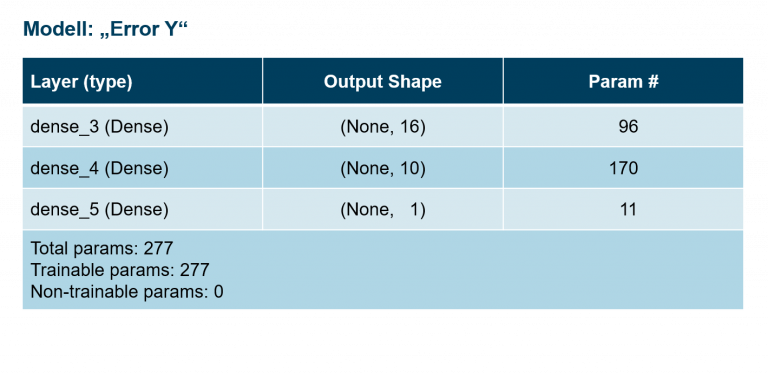
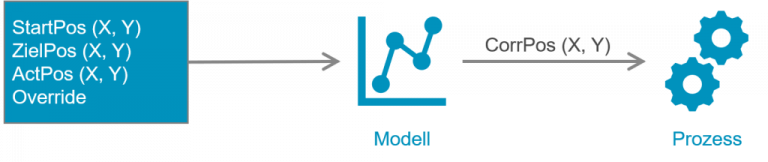
Vierter Schritt: Bereitstellung
Das mit Python entwickelte und trainierte Machine Learning Modell musste nun dem Roboter bzw. seiner Steuerung zur Verfügung gestellt werden. Hierfür haben wir eine Software entwickelt, welche herkömmliche Modellformate laden kann und mit einem OPC UA Interface ausstattet. Vorhersageanfragen an das Modell erfolgen somit über ein in der Industrie standardisiertes Kommunikationsprotokoll. Mittels den UA Methods (RPS im OPC UA Context) wird das Modell aufgerufen. Diese Lösung ist allerdings nur praktikabel, wenn die Abfrage nicht in Echtzeit erfolgen muss, da OPC UA nicht echtzeitfähig ist. Für unseren Fall war das tolerierbar, da der Roboter die Korrektur stets zu Beginn einer Bewegung anfordert und nicht während der Fahrt. Die Round-Trip-Time für den Aufruf war in der Regel sehr schnell und lag im niedrigen Millisekunden Bereich. Das Modell-Deployment als Web-Service zeichnet sich durch die lose Koppelung aus und ist daher auch einfach in die DevOps/ MLOps Pipeline integrierbar.

Ergebnisse
Nachdem dem Roboter das Modell, welches anhand der Testdaten am besten abgeschnitten hat (d.h. den kleinsten Vorhersagefehler aufwies) zur Verfügung stand, haben wir mit dessen Korrekturwerten Testfahrten durchgeführt und mit der Kamera den verbliebenen Positionierungsfehler gemessen. Bei den Testfahrten wurden jedoch nicht die gleichen Positionen wie bei der Erstellung der Trainingsdaten angefahren, sondern dem Modell unbekannte Positionen, um so die Fähigkeit der Generalisierung zu überprüfen. Die Abbildung zeigt die Positionierungsfehler auf der Kalibrierplatte mit Korrektur und ohne Korrektur im Vergleich. Im Großen und Ganzen konnte der Fehler durchschnittlich von 114 μm um 54 % auf 62 μm reduziert werden. Die Standardabweichung ist ähnlich geblieben (Verbesserung um ca. 10 %), da sie eher das Maß der Wiederholgenauigkeit ausdrückt. Für die meisten Testpunkte konnte der Fehler deutlich reduziert werden. Auffällig ist jedoch, dass das Modell für die unterste Zeile nicht so gut funktioniert. Die Modellentscheidungen von neuronalen Netzen sind nicht klar nachvollziehbar, da sich die gelernten Modellparameter nur schlecht bis gar nicht interpretieren lassen. So kann es für einzelne Testpunkte vorkommen, dass der Positionierungsfehler mit Korrektur unter Umständen größer wird als ohne Korrektur.

Abweichungen zwischen IST- und SOLL-Position ohne Korrektur
Abweichungen zwischen IST- und SOLL-Position mit Korrektur
Vorteile durch die Optimierung der Positioniergenauigkeit mit Machine Learning
Ein für den benötigten Arbeitsraum hinreichend genau getestetes Modell bringt entscheidende Vorteile gegenüber einer klassischen, regelbasierten Lösung:
-
- Aufwertung der Roboterhardware hinsichtlich Genauigkeit und/oder Performance durch eine Machine Learning Lösung („nur“ Software)
- Das Modell benötigt im laufenden Betrieb weder zusätzliche Hardware noch eine Bildverarbeitung. Lediglich in der Trainingsphase wird das Messsystem (Kamerasystem) benötigt. Regelbasierte Lösungen dagegen benötigen dauerhaft ein Positionsmesssystem (mit Bildverarbeitung). Bei manchen Prozessen, wie z. B. beim Schweißen, ist eine Bildverarbeitung nicht möglich bis stark eingeschränkt nutzbar.
- Das Modell benötigt im laufenden Betrieb weder zusätzliche Hardware noch eine Bildverarbeitung. Lediglich in der Trainingsphase wird das Messsystem (Kamerasystem) benötigt. Regelbasierte Lösungen dagegen benötigen dauerhaft ein Positionsmesssystem (mit Bildverarbeitung). Bei manchen Prozessen, wie z. B. beim Schweißen, ist eine Bildverarbeitung nicht möglich bis stark eingeschränkt nutzbar.
- Die Korrektur wird direkt auf die Zielkoordinaten angewendet – somit muss nicht „zeitaufwendig“ nachgeregelt werden. Die Taktzeit bleibt unverändert! Der Aufruf des Modells kann mit entsprechender Hardware auf wenige Millisekunden bis Nanosekunden optimiert werden.
- Bestandsmaschinen können nachgerüstet werden und in Betrieb bleiben: Die Optimierung erfolgt durch Beobachten von außen, ohne aktiv in den Prozess einzugreifen
- Durch „Transfer Learning“ ist das Modell auf Roboter verschiedener Hersteller übertragbar.
Fazit
Es kommt im Einzelfall immer auf die Art des Problems und die Beschaffenheit der Daten an, ob eine Lösung mit dem Machine Learning Ansatz sinnvoll ist und auch funktioniert. In manchen Fällen kann eine klassische Lösung (hier z. B. mit Kamerasystem und Nachregulierung) auch einfacher und genauer sein. Es gibt jedoch viele Bereiche, darunter Bildklassifizierung, Objekterkennung, Zeitreihen-Vorhersagen oder Klassifizierung, in denen Machine Learning aufgrund der Verschiedenartigkeit der Daten und der großen Anzahl an Dimensionen sehr gute Ergebnisse erzielt.











